Solow modeli temel yapısını açıklarken, nüfusun ve üretim teknolojisinin değişmediği varsayılacaktır. Yani çıktı emek ve sermaye girdilerine bağlı olarak değişir;
Y = F(K,L)
Solow büyüme modelinde tasarruf, sermaye birikimi ve büyüme arasındaki ilişki incelenirken, her şeyden önce sermayenin çıktı üzerindeki etkileri hesaba katılır. Bu bağlamda toplam üretim fonksiyonunun azalan verimler kanununa tabi olduğu, sermayenin ve emeğin marjinal ürününün giderek azaldığı ( emek miktarı sabit iken sermaye miktarı artınca her ilave birim sermayenin çıktıda meydana getireceği artışın giderek azaldığı veya tam tersine sermaye miktarı sabit iken emek miktarı artınca her ilave birim emeğin çıktıda meydana getireceği artışın giderek azaldığı ) varsayılır.
Ayrıca Solow büyüme modelinde sermayenin çıktı üzerindeki etkileri incelenirken, toplam üretim fonksiyonunun ölçeğe göre sabit getiriye tabi olduğu, örneğin sermaye ve emek girdilerinin miktarı 2 kat arttığında çıktının da 2 kat arttığı kabul edilir;
2Y = F ( 2K, 2L )
xY = F ( xK, xL )
Solow büyüme modelinde ölçeğe göre sabit getiri varsayımı altında girdilerin 1/L oranında arttığı kabul edilmek üzere, toplam üretim fonksiyonu aşağıdaki gibi yazılır;
Y/L = F ( K/L,1 )
Y/L = F ( K,L )
y = f (k)
Bu denkleme göre, işçi başına çıktı ( y = Y/L ) işçi başına sermayeye ( k = K/L ) bağlı olarak değişir. Bu durum aşağıdaki grafikte gösterilmiştir;
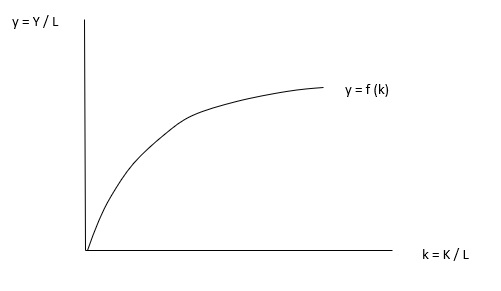
Grafikte üretim fonksiyonunu, işçi başına sermaye arttıkça işçi başına çıktının da arttığını, ancak azalan verimler kanunu nedeniyle sermayedeki artışın çıktıda giderek daha az bir artışa yol açtığını göstermektedir.
Solow büyüme modelinde büyüme, sermaye birikimi ve tasarruf arasındaki ilişki incelenir. Sermayenin çıktı üzerindeki etkileri yanında çıktının sermaye birikim üzerindeki etkileri de hesaba katılır. Bu anlamda Solow modelinin hareket noktası, hükümetin olmadığı kapalı bir ekonomide çıktının tüketim ve yatırım amacıyla kullanıldığı hususudur;
Y = C + I
Y/L = C/L +I/L
y = c+i
olow büyüme modelinde kişilerin gelirlerinin s kadarlık bir bölümünü tasarruf ettikleri geri kalan ( 1- s ) kadarlık bir bölümünü de tüketim amacıyla kullandıkları varsayıldığından, C = (1-s)Y, işçi başına tüketim fonksiyonu aşağıdaki gibi ifade edilebilir;
C/L = (1-s) Y/L
c = (1-s)y
y = (1-s)y+i
i = sy
Bu denkleme göre, işçi başına yatırım tasarruf haddi ile işçi başına çıktının çarpımından ibaret olan işçi başına tasarrufa eşittir, kısaca tasarruf yatırıma eşittir ( I = S ).
Diğer taraftan belirli bir dönemde işçi başına sermaye stokunda meydana gelen değişme, o dönemde yapılan işçi başına yatırım ile o dönemde işçi başına sermaye stokunda meydana gelen yıpranma arasındaki farka, kısaca o dönemdeki işçi başına net yatırıma eşittir;
Δk = i dk
Δk = sf(k) -dk
Bu denkleme göre işçi başına sermaye düzeyi ( k ) ne kadar büyük olursa, işçi başına tasarruf – yatırım ve işçi başına yıpranma da o kadar büyük olur.
Solow modelinde eğer ekonominin başlangıçta sahip olduğu işçi başına sermaye düzeyi durağan durum sermaye düzeyinden küçük ise (k < k*) , işçi başına sermaye düzeyi artar ve ekonomi nihayet durağan duruma (k = k*) ) ulaşır. Buna karşılık bir ekonominin başlangıçta sahip olduğu işçi başına sermaye düzeyi durağan durum sermaye düzeyinden büyük ise (k > k*), işçi başına sermaye düzeyinin giderek azalması sonucu ekonomi yine durağan duruma ulaşır.
Solow büyüme modeli, özellikle uzun dönemli ekonomik büyümenin kaynaklarını anlamak açısından modern iktisat literatürünün en temel teorik çerçevelerinden biridir. Modelin en önemli katkısı, tasarruf oranları, sermaye birikimi, yıpranma (depreciation) ve üretim teknolojisi arasındaki ilişkiyi açık ve sistematik bir biçimde ortaya koymasıdır. Keynesyen kısa dönemli analizlerden farklı olarak Solow modeli, ekonomilerin zaman içinde nasıl bir dengeye ulaştıklarını ve büyüme sürecinde hangi unsurların kalıcı, hangilerinin geçici etkiler doğurduğunu açıklamayı amaçlar.
Modelde vurgulanan ilk kritik nokta, azalan verimler kanununun büyüme sürecine getirdiği sınırlardır. Sermaye birikimi başlangıçta üretim artışlarını hızlandırır, fakat belirli bir seviyeden sonra eklenen her yeni sermaye biriminin sağladığı katkı giderek azalır. Bu nedenle sürekli sermaye artışı tek başına ekonominin sınırsız büyümesini sağlayamaz. Buradan çıkan sonuç, uzun dönemli büyümenin yalnızca tasarruf oranlarının artırılması veya sermaye stokunun yükseltilmesi ile sürdürülemeyeceğidir. Bu yaklaşım, kalkınma politikalarında tasarruf ve yatırım oranlarını artırmaya yönelik çabaların önemini kabul etmekle birlikte, tek başına yeterli olmadığını ortaya koyar.
İkinci önemli sonuç, durağan durum (steady state) kavramıdır. Solow modelinde her ekonomi, işçi başına sermaye düzeyinde belirli bir noktaya ulaştığında net yatırım sıfırlanır. Bu durumda sermaye stokundaki artış ile yıpranma birbirini dengelediği için sermaye birikimi daha fazla büyüme yaratmaz. Durağan durumda kişi başına sermaye ve kişi başına çıktı sabitlenir. Bununla birlikte, toplam çıktı nüfus artışı kadar büyümeye devam edebilir. Durağan durum, ekonominin iç dinamiklerinden kaynaklanan uzun dönem denge büyüme yolunu temsil eder ve farklı ülkelerin kişi başına gelir seviyelerindeki farklılıkları açıklamada kilit bir rol oynar.
Üçüncü olarak, Solow modelinin en çarpıcı yönlerinden biri teknolojinin dışsal kabul edilmesidir. Modelde teknolojik gelişme olmadığı varsayıldığında, kişi başına gelir düzeyi durağan durumda sabit kalır. Oysa teknolojik gelişme eklendiğinde, üretim fonksiyonu yukarı doğru kayar ve kişi başına çıktı sürekli artar. Böylece uzun dönemli ekonomik büyümenin en temel kaynağı olarak teknoloji öne çıkar. Bu sonuç, modern iktisadi büyüme teorilerinin (örneğin içsel büyüme modellerinin) gelişmesine zemin hazırlamıştır.
Solow modeli aynı zamanda “yakınsama hipotezi” (convergence hypothesis) ile de bilinir. Bu hipoteze göre benzer tasarruf oranlarına, nüfus artış hızına ve teknolojik gelişme oranına sahip ülkeler, uzun vadede benzer kişi başına gelir seviyelerine yakınsar. Bu, düşük sermaye stokuna sahip ülkelerin daha hızlı büyüme potansiyeline sahip olduğu anlamına gelir çünkü azalan verimler kuralı gereği sermayenin marjinal verimliliği bu ülkelerde daha yüksektir. Ancak ampirik bulgular, bu yakınsamanın mutlak değil, koşullu olduğunu göstermektedir. Yani ülkelerin aynı yapısal özelliklere sahip olmaları durumunda yakınsama gerçekleşir. Aksi halde, kurumlar, eğitim düzeyi, teknolojiye erişim gibi faktörler farklılık gösterdiğinde gelir farkları kalıcı hale gelir.
Bir başka önemli nokta, Solow modelinin politika önerileridir. Model, tasarruf oranlarının artırılmasının kısa ve orta vadede büyümeyi hızlandırabileceğini kabul eder. Ancak uzun vadede sürdürülebilir büyümenin yalnızca teknolojik yenilikler ve verimlilik artışları ile sağlanabileceğini gösterir. Bu nedenle eğitim, Ar-Ge yatırımları, kurumsal yapıların güçlendirilmesi gibi unsurlar büyüme politikalarında öncelikli hale gelir. Böylece model, kalkınma iktisadı açısından da yol gösterici bir çerçeve sunar.
Ayrıca Solow modeli, üretim fonksiyonunun ölçeğe göre sabit getiriler varsayımı altında kurgulandığı için sermaye ve emek arasındaki dağılımı da açıklamada kullanılır. Gelir dağılımındaki farklılıkların uzun vadeli büyüme üzerindeki etkilerini analiz ederken, faktör gelir paylarının nasıl evrildiğini ortaya koyar. Bu özellik, gelir dağılımı çalışmalarına önemli bir teorik temel sağlamıştır.
Son olarak, Solow modelinin sınırlılıkları da dikkate alınmalıdır. Modelde teknoloji dışsal kabul edildiği için teknolojik ilerlemenin nedenlerini açıklamaz. Ayrıca finansal piyasalar, beşeri sermaye birikimi, kurumsal faktörler gibi büyüme sürecinde kritik öneme sahip unsurları dışarıda bırakır. Bu nedenle sonraki yıllarda Romer, Lucas gibi iktisatçılar içsel büyüme modellerini geliştirmiş, teknolojik ilerlemenin ve bilgi birikiminin ekonominin iç dinamikleri tarafından nasıl üretildiğini göstermeye çalışmışlardır. Buna rağmen, Solow modeli hem teorik açıdan hem de pratik politika analizlerinde hâlâ en çok kullanılan çerçevelerden biridir.