Veri analizinde en sık kullanılan yöntemlerden biri regresyondur, Lasso regresyonu da bu regresyon türlerinden biridir. Regresyon, bir bağımlı değişkeni bu değişkenin veri setindeki diğer bağımsız değişkenlerle arasındaki ilişkisini kullanarak tahmin etmeyi sağlayan bir istatiksel metottur. En temel regresyon türü bağımlı bir değişken ile bağımsız değişkenler arasındaki ilişkiyi doğrusal bir şekilde modelleyen lineer regresyondur.
Gerçek hayattaki veri setleri genellikle karmaşık ve çok boyutludur. Böyle durumlarda klasik doğrusal regresyon çoğu zaman yetersiz kalır. Örneğin değişkenler arasında yüksek korelasyon varsa katsayılar kararsız hale gelir(multicollinearity). Ya da çok sayıda değişken varsa model overfitting(aşırı uyum) riski taşır. Bu sebeplerden ötürü eğitim verisinde iyi görünen ama yeni veride başarısız olan tahminler ortaya çıkabilir. Bu sorunlar tahmin performansının düşmesine ve genelleme gücünün zayıflamasına yol açar.
İşte bu noktada Lasso ve Ridge regresyonları devreye girer. Lasso ve Ridge regresyonları klasik doğrusal regresyona bir ceza terimi(penalty/regularization term) ekleyerek katsayıların büyüklüğünü sınırlar. Böylece modelin hem daha dengeli hem de daha genellenebilir olmasını sağlar. Özellikle çok sayıda değişkenin olduğu ve değişkenler arasında yüksek korelasyon bulunan veri setlerinde Lasso ve Ridge regresyonları güçlü alternatifler olarak öne çıkar.
Klasik doğrusal regresyon modeli şu şekildedir:

Klasik regresyonda kullanılan en küçük kareler (OLS) yöntemi, β katsayılarını şu fonksiyonu minimize ederek tahmin eder:
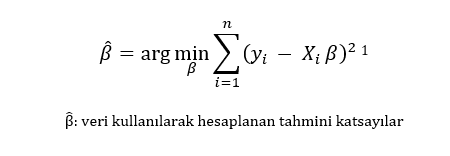
Ancak bu yaklaşım multicollinearity veya çok sayıda bağımsız değişken olduğunda kararsız sonuçlar verebilir. İşte bu nedenle değişkenler arası korelasyondan kaynaklı hatayı daha aza indirgemek için bu korelasyonu tabiri caizse cezalandıran Lasso ve Ridge regresyonları devreye girer.
Lasso Regresyonunun Matematiksel Arka Planı
Lasso(Least Absolute Shrinkage and Selection Operator) regresyonu, klasik doğrusal regresyona L1 ceza terimi ekleyerek katsayıların büyüklüğünü sınırlar. Amaç fonksiyonu şu şekilde yazılır:
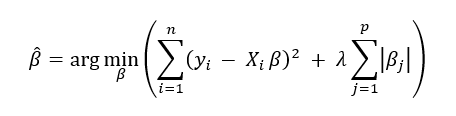
Buradaki toplama işaretinden sonra eklenen ve λ ile başlayan ifade L1 ceza terimi olarak adlandırılır. Bu ceza katsayıların yalnızca küçülmesini değil, aynı zamanda bazılarının, bazen tamamen sıfıra inmesini sağlar. Böylece model, bazı değişkenleri tamamen ortadan kaldırarak değişken seçimi(feature selection) yapabilir. Lasso regresyonu önemsiz değişkenlerin etkisini azaltarak veya tamamen elemine ederek değişken seçimi yapar. Böylece daha basit ve yorumlanabilir bir model sunar. Boyut indirgeme için sıklıkla tercih edilir. Ancak tüm değişkenlerin önemli olduğu durumlarda doğruluk istenildiği kadar stabil olmayabilir, bazı değişkenleri tamamen sıfırlamak performansı düşürebilir. Ayrıca λ değeri küçüldükçe cezanın ağırlığı azalır ve dolayısıyla amaç fonksiyonu da OLS’ye yakınsar. λ değeri çok büyük olursa da ceza terimi çok baskın hale gelir ve katsayılar sıfıra yakınsar.
Ridge Regresyonunun Matematiksel Arka Planı
Ridge regresyonunun amaç fonksiyonu:
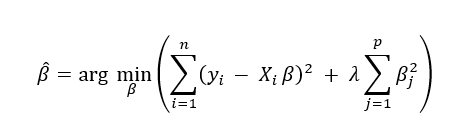
Burada eklenen toplama işaretinden sonra eklenen λ ifadesi ise L2 ceza terimi olarak adlandırılır. Bu ceza katsayıların yalnızca küçülmesini sağlar. Yani L1 cezasından farklı olarak katsayıların tam olarak sıfıra inmesine genellikle yol açmaz. Dolayısıyla Ridge regresyonu, tüm değişkenleri modelde tutar fakat katsayıların büyüklüklerini sınırlandırarak overfitting’i engeller ve multicollinearity durumlarında daha kararlı tahminler elde edilmesine yardımcı olur. Ridge regresyonu değişkenler arasında yüksek korelasyon bulunduğu durumlarda katsayıları küçülterek kararsızlığı azaltır. Ayrıca ceza terimi sayesinde modelin karmaşıklığını azaltır. Özellikle çok değişkenli ve gürültülü veri setlerinde klasik regresyona göre daha az hata verir. Lasso regresyonundan farklı olarak da katsayıları küçültse de sıfırlamadığı için her değişkenin etkisini ele almış olur. Ancak aynı sebepten ötürü değişkenleri sıfırlayarak değişken seçimi yapamaz. λ seçimi burada da önemlidir. λ çok küçük olursa ridge regresyonu da Lasso regresyonu ile aynı şekilde klasik regresyon gibi davranır, λ çok büyük olursa da ceza terimi baskın hale gelir ve katsayılar sıfıra yaklaşır ve model aşırı basitleşir. En uygun λ değerini bulmak için genellikle cross-validation gerekir.
Elastic Net
Lasso ve Ridge regresyonlarının avantajlarını bir araya getiren Elastic Net yöntemi de pratikte sıkça tercih edilir. Elastic Net, hem L1 (Lasso) hem de L2 (Ridge) ceza terimlerini birleştirerek çalışır. Böylece hem değişken seçimi yapılabilir hem de katsayı kararlılığı sağlanır. Özellikle yüksek boyutlu ve korelasyonlu veri setlerinde, yalnızca Lasso veya Ridge kullanmaya göre daha dengeli sonuçlar verir. Matematiksel formülü ise şöyledir:
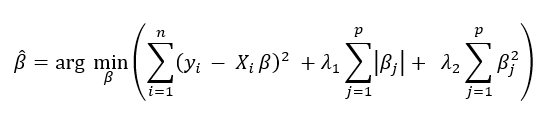
Sonuç olarak Lasso ve Ridge regresyonları, klasik doğrusal regresyonun karşılaştığı multicollinearity, overfitting ve genelleme sorunlarına güçlü çözümler sunar.
- Lasso regresyonu, bazı katsayıları sıfıra indirerek değişken seçimi yapabilmesi sayesinde daha yalın ve yorumlanabilir modeller üretir. Özellikle çok sayıda değişkenin bulunduğu ve boyut indirgeme gerektiren durumlarda öne çıkar.
- Ridge regresyonuise tüm değişkenleri modelde tutar, katsayıları küçülterek kararsızlığı azaltır ve tahmin performansını daha dengeli hale getirir. Özellikle değişkenlerin tamamının önemli olduğu ve yüksek korelasyon bulunan veri setlerinde tercih edilir.
Uygulamada hangi yöntemin seçileceği, veri setinin yapısına ve analizin amacına bağlıdır. Ayrıca, Lasso ve Ridge’in güçlü yanlarını birleştiren Elastic Net yaklaşımı da pratikte sıkça kullanılan bir alternatiftir.
Kısacası, Lasso ve Ridge regresyonları yalnızca istatistiksel bir teknik değil; aynı zamanda daha güvenilir, genellenebilir ve yorumlanabilir modeller kurmayı sağlayan modern veri analizi yöntemleridir.
[1] Argmin: Bir f(x) fonksiyonun minimum değerini aldığı x girdisini ifade eder.