İstatistik Modelleme

Günümüzde veri, her sektörde karar alma süreçlerinin merkezinde yer alıyor. Ancak verinin kendisi yalnızca bir başlangıçtır. Asıl önemli olan, bu verilerden anlam çıkarabilmek, geleceğe dair çıkarımlarda bulunabilmek ve belirsizlikleri yönetebilmektir. İşte bu noktada istatistik modelleme, güçlü bir araç olarak karşımıza çıkar.

İstatistiksel modelleme, veriyle bilinmeyeni anlamlandırmanın pusulasıdır. Dağılımlar, varyanslar, beklenen değerler ve olasılık teorisi gibi kavramlar aracılığıyla, sadece “ne oldu?” sorusuna değil, “neden oldu?” ve “bundan sonra ne olabilir?” sorularına da yanıt verir. Bu nedenle istatistiksel modelleme, veri biliminin matematiksel omurgasıdır.

Bu yazıda, istatistiksel modellemenin temel yapı taşlarını ele alacağız. Makine öğrenmesiyle olan ilişkisini açıklayacak; beklenen değer, varyans, olasılık dağılımları gibi kavramları örneklerle somutlaştıracağız. Ayrıca Bernoulli’den Dirichlet’e kadar farklı dağılımların hangi senaryolarda nasıl kullanıldığını göstererek, bu kavramların hem teorik hem pratik boyutlarını inceleyeceğiz.

İstatistiksel modelleme, verilerle olasılıksal ilişkiler kurarak hem bilinmeyen yapıları keşfetmek hem de geleceğe dair tahminlerde bulunmak için kullanılan güçlü bir yöntemdir. Bu modeller, hedef değişkenin bilinip bilinmemesine göre denetimli (supervised) ya da denetimsiz (unsupervised) olarak ikiye ayrılır.

Yöntemler:

1. Bayesian Modeling (Bayesyen Modelleme): Önceden bilinen bilgileri (prior) ve gözlemlenen verileri birleştirerek parametreler hakkında güncellenmiş olasılık (posterior) elde etmeyi amaçlayan olasılıksal modelleme yaklaşımıdır.
2. Decision Trees (Karar Ağaçları): Veriyi dallara ayırarak karar kuralları oluşturan ve sonuçlara ulaşan, görsel olarak da yorumlanabilir denetimli öğrenme algoritmasıdır.
3. Random Forest (Rastgele Orman): Birden fazla karar ağacının (decision tree) topluluğuyla çalışan, varyansı düşürüp aşırı öğrenmeyi azaltan güçlü bir topluluk öğrenmesi (ensemble) yöntemidir.
4. Gradient Boosting(Aşamalı Artırma): Zayıf öğrenicilerin (genellikle karar ağaçlarının) art arda eğitilerek hata payının adım adım azaltıldığı, yüksek doğruluğa sahip bir tahminleme yöntemidir.
5. K-means Clustering(K-ortalama kümeleme): Belirli sayıda küme merkezine (k) en yakın verileri gruplayan ve her veri noktasını en yakın merkeze atayan denetimsiz bir kümeleme algoritmasıdır.
6. Lineer Regresyon: Bağımlı ve bağımsız değişkenler arasındaki doğrusal ilişkiyi modelleyen ve sürekli değişkenleri tahmin etmek için kullanılan temel regresyon tekniğidir.
7. Lojistik Regresyon: Olasılık temelli sınıflandırma yapmak için kullanılan, özellikle ikili(binary) sınıflandırma problemlerinde yaygın olarak tercih edilen regresyon türüdür.
8. Principal Component Analysis(Temel Bileşenler Analizi): Çok boyutlu verideki temel yapıyı ortaya çıkarmak ve boyut indirgeme yapmak için kullanılan istatistiksel bir dönüşüm tekniğidir.
9. DBSCAN(Yoğunluk Tabanlı Kümeleme): Yoğunluk tabanlı, küme sayısını önceden belirlemeye gerek duymayan, gürültüye ve şekil çeşitliliğine duyarlı bir denetimsiz öğrenme algoritmasıdır.

 

Makine Öğrenmesi Algoritma Türleri

Makine öğrenmesi, verinin yapısına ve probleme yaklaşım biçimine göre dört ana kategoriye ayrılır: denetimli öğrenme, denetimsiz öğrenme, yarı denetimli öğrenme ve pekiştirmeli öğrenme.

Denetimli öğrenme, hem giriş (X) hem de doğru çıkış (Y) verisinin bulunduğu durumlarda kullanılır. Model, bu veriler üzerinden öğrenerek yeni gelen veriler için doğru tahminler yapmayı amaçlar. Örneğin, geçmiş konut satış verilerine bakarak yeni bir evin fiyatını tahmin etmek bu kapsama girer.

Denetimsiz öğrenme, yalnızca giriş verisiyle çalışır; yani etiketli veri (Y) yoktur. Bu durumda model, verinin iç yapısını analiz ederek kümeleri, benzerlikleri veya kalıpları keşfetmeye çalışır. Müşteri segmentasyonu ve boyut indirgeme teknikleri bu türdendir.

Yarı denetimli öğrenme, verilerin bir kısmı etiketliyken büyük bir kısmı etiketsiz olduğunda kullanılır. Bu model, etiketsiz veriyi de eğitime dahil ederek daha güçlü sonuçlar elde etmeye çalışır. Etiketlemenin maliyetli olduğu senaryolarda oldukça pratiktir.

Pekiştirmeli öğrenme ise bir ajanın çevresiyle etkileşim kurarak ödül topladığı ve zamanla en iyi stratejiyi öğrenmeye çalıştığı bir yaklaşımdır. Oyun oynayan yapay zeka sistemleri veya otonom araç kontrol sistemleri bu kategoriye örnek verilebilir.

İndikatör Fonksiyon:  

Bir küme A için indikatör fonksiyon I_A(x), eleman x‘in bu kümede olup olmadığını kontrol eder ve şöyle tanımlanır:

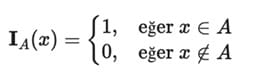
Beklenen Değer(Expected Value)

Beklenen değer (diğer adıyla beklenti ya da ortalama), bir rassal değişken X’in E(X) ile gösterilen ortalama değeridir.

Bu, X’in alabileceği tüm değerlerin, bu değerlerin olasılıkları ile ağırlıklandırılmış ortalamasıdır.

Eğer X ayrık bir değişkense:

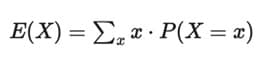
veya:

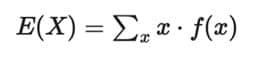
Eğer X sürekli bir değişkense ve olasılık yoğunluk fonksiyonu (PDF) f(x) ile tanımlanmışsa, toplam yerine integral alınır:

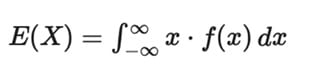
Varyans

Bir rassal değişkenin varyansı, değerlerinin ne kadar yayıldığını ölçer.

Eğer X ortalaması E(X) = μ olan bir rassal değişkense, varyans E[(X – μ)²] olarak tanımlanır.

Başka bir deyişle, X’in ortalamasından sapmasının karesinin beklenen değeridir.

Eğer X ayrık bir değişkense, varyans şu şekilde hesaplanır:

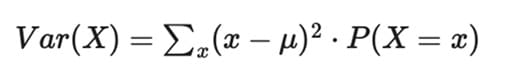
ve eğer X sürekli ise:

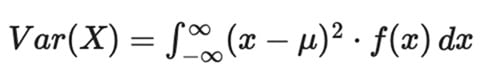
Argmax

Eğer elimizde bir fonksiyon f(x) varsa:

argmax_x f(x)

anlamı:

f(x) fonksiyonunun maksimum değerini aldığı x değeri (veya değerlerini) bul.

Likelihood (Olabilirlik)

Verilen bir model parametresi altında gözlemlenen verinin meydana gelme olasılığıdır.

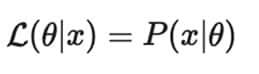
Log-Likelihood(Log-Olabilirlik)

Olasılıkların çarpımı yerine toplamı alınarak hesaplama kolaylaştırılır.

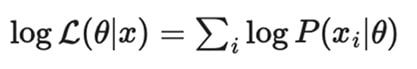
Maximum Likelihood Estimation (En Yüksek Olabilirlik Tahmini)

Gözlemlenen veri için likelihood fonksiyonunu maksimize eden parametre  θ‘yı bulma yöntemidir.

Bayesian Likelihood (Posterior, Güncellenmiş Olabilirlik) 

Bayes Teoremi kullanılarak parametre hakkında ön bilgiyle birlikte güncellenmiş olasılık elde edilir:

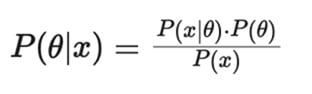
Kümülatif Dağılım Fonksiyonu (CDF)

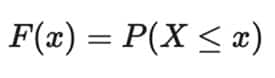
Burada X rassal bir değişkendir.

Eğer X ayrık ise, CDF şu şekilde hesaplanır:

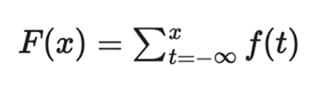
Burada f(t) = P(X = t), yani olasılık kütle fonksiyonudur (PMF).

Eğer X sürekli bir değişkense:

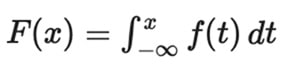
Burada  f(t), olasılık yoğunluk fonksiyonudur(PDF).

Kantil (Quantile) Fonksiyonu

Kümülatif dağılım fonksiyonu (CDF), bir rassal değişken için bir değer alır ve buna karşılık gelen bir olasılık döndürür.

Bunun yerine, 0 ile 1 arasında bir sayı (örneğin p) ile başlayıp,

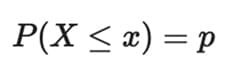
eşitliğini sağlayan x değerini bulmak istediğimizi düşünelim.

Bu eşitliği sağlayan x değeri, p kantili (ya da dağılımın %100 p yüzdelik dilimi) olarak adlandırılır.

 

Bayesian Modeling:

 

Bayesyen modelleme, ön bilgi (prior) ile gözlemlenen verileri (data/likelihood) birleştirerek güncellenmiş bilgi (posterior) elde etmeye dayanır.

 

Bayes Teoremi

Modelleme aşamaları:

1. Prior belirleme
2. Likelihood
3. Posterior hesaplama

Dağılım Türleri:

1. Bernoulli(Geometrik) Dağılımı

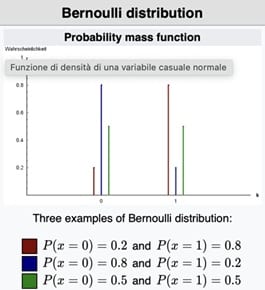
Bernoulli dağılımı, yalnızca iki olası sonucu olan deneyleri modellemek için kullanılır. Bu sonuçlar genellikle “başarı” ve “başarısızlık” (veya 1 ve 0) olarak temsil edilir.

Binary sınıflandırma problemleri, başarı-olasılık modelleri, kullanıcı davranış tahmini gibi durumlarda kullanılır. Bir madeni para atıldığında yazı gelmesini “başarı (1)” ve tura gelmesini “başarısızlık (0)” olarak kodlayalım. Eğer para adilse, başarı olasılığı p = 0.5’tir. Bu deney Bernoulli dağılımı ile modellenebilir çünkü:

• Deney yalnızca bir kez yapılır.
• Sonuçlar ikilidir (yazı ya da tura).
• Her bir atış birbirinden bağımsızdır.

Parametre: p ∈ [0,1]

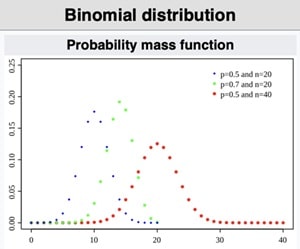
2. Binomial Dağılımı

Binom dağılımı, aynı Bernoulli deneyinin birden fazla kez (n kez) tekrarlanmasıyla oluşan toplam başarı sayısını modellemek için kullanılır. Başarı sayısının hesaplandığı durumlar, A/B testleri, kalite kontrol uygulamaları gibi alanlarda kullanılır. Örneğin bir ürünün kalite kontrol testinde, her biri bağımsız 10 test yapılır ve her testte ürünün hatasız çıkma olasılığı olarak bilinir. Bu durumda, 10 testte kaç tanesinin hatasız çıkacağını modellemek için binom dağılımı kullanılır. Binom dağılımı, Bernoulli dağılımının çoklu tekrarı olarak düşünülebilir.

Parametre: n(deneme sayısı),  p(başarı olasılığı)

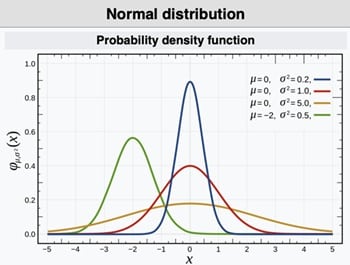
3. Normal (Gaussian) Dağılım

Normal dağılım, sürekli veri noktalarının bir ortalama etrafında simetrik olarak dağılmasıyla oluşan dağılımdır. Çan eğrisi(bell curve) olarak da bilinir. Doğal olayların çoğu (boy uzunluğu, sınav puanı, üretim hataları vb.) normal dağılıma yakındır. Ayrıca birçok istatistiksel testin ve regresyon modelinin temel varsayımıdır. Mesela bir üniversitede 1000 öğrencinin sınavdan aldığı notlar ortalama 70, standart sapma 10 olsun. Bu durumda, not dağılımı yaklaşık olarak normal dağılıma uyar. Öğrencilerin büyük bir kısmı 60-80 aralığında not alırken, uç değerler daha az görülür. Ayrıca normal dağılımın önemli bir özelliği de Merkezi Limit Teoremi sayesinde, yeterince büyük örneklemlerden elde edilen ortalamaların normal dağılıma yakınsamasıdır.

Parametre: μ(ortalama), σ²(varyans)

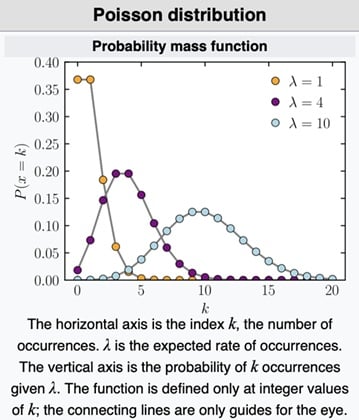
4. Poisson Dağılımı

Poisson dağılımı, belirli bir zaman aralığında veya sabit bir alanda meydana gelen olayların sayısını modellemek için kullanılır. Bu olaylar nadir ve bağımsız olarak gerçekleşir. Sayılabilir olayların modellenmesinde yaygın olarak kullanılır. Örneğin bir banka şubesine bir saatte ortalama 5 müşteri gelmektedir. Bu durumda, bir saatte tam olarak 3 müşteri gelme olasılığı Poisson dağılımı ile hesaplanabilir. Poisson dağılımı, olayların nadir ama düzenli aralıklarla gerçekleştiği durumlar için idealdir.

Parametre: λ>0 (Belirli bir aralıktaki beklenen ortalama olay sayısı)

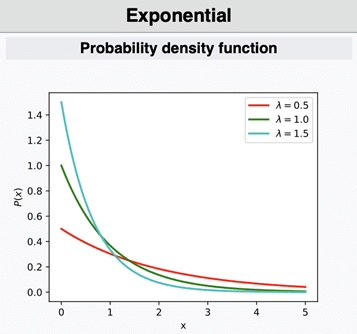
5. Exponential(Üstel) Dağılım

Üstel dağılım, iki olay arasındaki süreyi modellemek için kullanılır. Bir olayın meydana gelmesini bekleme süresinin olasılık dağılımını ifade eder. Arızalanma süreleri, müşteri geliş aralıkları, servis süreleri gibi olaylar arasında geçen zamanın modellenmesinde kullanılır. Örneğin bir ATM’ye ortalama olarak her 10 dakikada bir müşteri geliyorsa, bir sonraki müşterinin geliş süresi üstel dağılım ile modellenebilir. Ayrıca üstel dağılım Poisson sürecinde olaylar arası zaman aralıklarının dağılımıdır.

Parametre: λ(Olayın birim zamanda gerçekleşme oranı(rate))

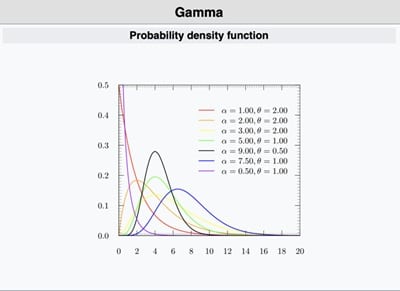
6. Gamma Dağılımı

Gamma dağılımı, pozitif sürekli değerli verileri modellemek için kullanılan esnek bir dağılımdır. Üstel dağılımın genelleştirilmiş halidir ve olaylar arası toplam sürenin modellemesinde kullanılır. Varyans modelleme, bekleme süresi birikimi, Poisson dağılımlarında prior olarak kullanımı gibi alanlarda kullanılır. Bir çağrı merkezinde, arka arkaya 3 çağrının gelmesi için geçen toplam süreyi modellemek istiyorsak ve her çağrı gelişi bağımsız şekilde üstel dağılıma uyuyorsa, bu toplam süre Gamma dağılımı ile modellenebilir. Ayrıca α = 1 durumunda Gamma dağılımı, üstel dağılıma eşit olur.

Parametre: α (şekil), β (ölçek)

7. Beta Dağılımı

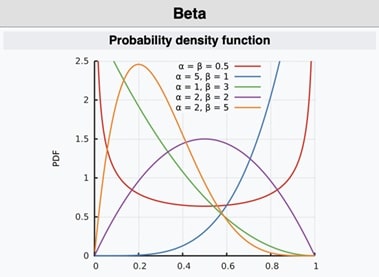
Beta dağılımı, 0 ile 1 arasında yer alan sürekli değerli olasılıkların modellenmesinde kullanılır. Özellikle başarı oranlarını modellemek için uygundur. Bernoulli ve Binom dağılımları için öncül(prior) dağılım olarak Bayesyen istatistikte yaygın şekilde kullanılır. Ayrıca oran verileri(örneğin başarı yüzdesi) için de uygundur. Örneğin bir e-ticaret sitesinde yeni bir ürün sayfası için tıklama oranı ölçülmek isteniyor diyelim. İlk etapta çok az veri olduğunda, öncül bilgi olarak Beta(1,1) (yani eşit dağılımlı ve belirsiz) kullanılabilir. Daha fazla veri geldikçe dağılım güncellenir. Ayrıca α=β=1 olduğunda Beta dağılımı Uniform(0,1) dağılımına eşit olur.

Parametre: α, β   

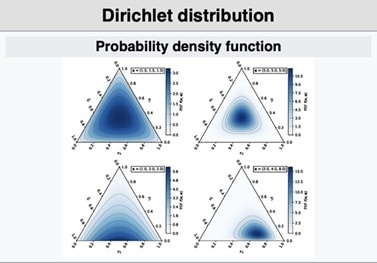
8. Dirichlet Dağılımı

Dirichlet dağılımı, Beta dağılımının çok değişkenli (multinom) genelleştirilmiş halidir. 0 ile 1 arasında kalan, toplamı 1 olan birden fazla oranın ortak dağılımını tanımlar. Bayesyen modellemede, özellikle çok sınıflı (kategorik) dağılımların öncül (prior) bilgisi olarak kullanılır. Konu modelleme, karışım modelleri ve sınıflandırma gibi çok kategorili problemlerde sıkça tercih edilir. Örneğin bir haber sitesinde ziyaretçilerin ilgilendiği kategoriler üzerine yapılan analizlerde, kullanıcıların bu kategorilere olan eğilimlerini modellemek için Dirichlet dağılımı kullanılabilir. Her kategoriye ilişkin oranlar toplamda 1 olacak şekilde ifade edilir. Ayrıca K = 2 olduğunda Dirichlet dağılımı Beta dağılımına indirgenir.

Parametre: α₁,α₂,…, α_K

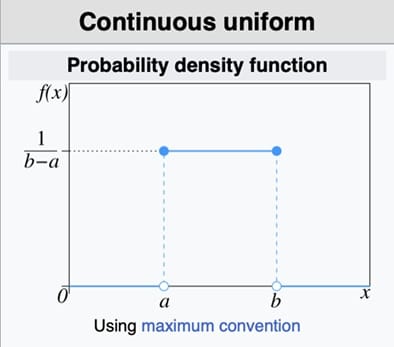
9. Uniform Dağılım

Uniform dağılım, belirli bir aralıkta tüm değerlerin eşit olasılıkla gerçekleştiği dağılımdır. Sürekli ve ayrık versiyonları vardır. Simülasyonlar, rastgele sayı üretimi, belirsizliğin modellendiği durumlar ve Bayesyen analizlerde öncül dağılım olarak kullanılır. Örneğin bir oyunda kullanıcının rastgele bir ödül kazanması için sistem 1 ile 100 arasında eşit olasılıkla bir sayı seçtiğini düşünelim. Bu seçim Uniform(a=1, b=100) dağılımı ile modellenebilir. Ayrıca Uniform(0,1) dağılımı birçok başka dağılımın türetilmesinde temel olarak kullanılır.

Parametre: a → minimum değer, b → maksimum değer

Merkezi Limit Teoremi(Central Limit Theorem):   

 

X₁, X₂, …, Xₙ bağımsız ve aynı dağılıma sahip, ortalaması μ ve varyansı σ² olan rassal değişkenler olsun. Merkezi Limit Teoremi‘ne göre, n arttıkça (yani örneklem büyüdükçe), bu değişkenlerin örneklem ortalaması, yaklaşık olarak ortalaması μ ve varyansı σ²/n olan bir normal dağılıma yakınsar.

 

Merkezi Limit Teoremi, istatistikte en önemli kavramlardan biridir. Temel olarak şunu söyler: Eğer aynı dağılıma sahip, bağımsız rastgele değişkenlerden oluşan yeterince büyük bir örneklem alırsanız, bu örneklemlerin ortalamaları neredeyse her zaman normal dağılıma yaklaşır, orijinal dağılım ne olursa olsun! Örneğin, bir kafede sipariş verilen kahve hazırlama süresi çok düzensiz dağılmış olabilir. Ancak bu sürelerden rastgele 50 tanesinin ortalamasını alırsanız, bu ortalama değerler normal dağılıma oldukça yakınsar. Bu özellik, birçok istatistiksel testin ve güven aralığının temel dayanağıdır.

 

Bu yazıda, istatistiksel modellemenin temel kavramlarını hem teorik hem pratik yönleriyle ele aldık. Beklenen değer, varyans, olasılık dağılımları ve merkezi limit teoremi gibi kavramlar sayesinde verilerden nasıl anlam çıkarabileceğimizi gördük. Ayrıca farklı dağılımların hangi durumlarda kullanıldığını öğrenerek, istatistiksel düşünme biçiminin temellerini pekiştirdik.

Veri bilimi, sadece algoritmaları çalıştırmak değil; aynı zamanda verinin doğasını anlayarak doğru modelleri kurmaktır. İstatistiksel dağılımlar bu yolculukta bize oldukça yön verir. Doğru dağılımı seçmek, modelin doğruluğunu artırırken yorumlanabilirliğini de güçlendirir. İstatistiksel modelleme konusundaki bu temel bilgiler, veriyle çalışan herkes için vazgeçilmezdir.