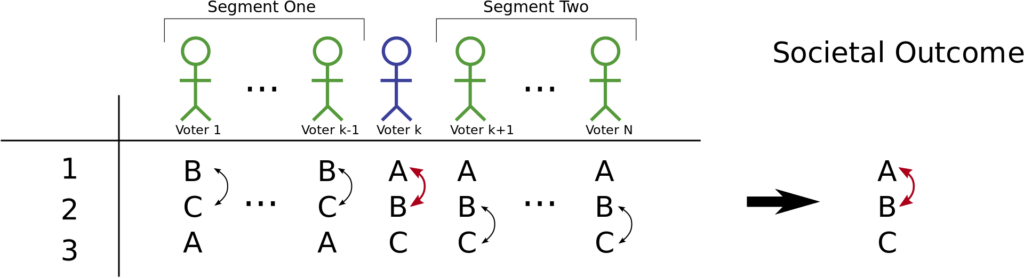Arrow İmkansızlık Teoremi Nedir? Pareto optimal dağılımlardan hangisinin diğerlerinden daha üstün olduğunu ve dolayısıyla da diğerlerine tercih edilmesi gerektiğini belirlemeyi mümkün kılan sosyal refah fonksiyonu yaklaşımının temel güçlüğü, demokratik bir ortamda sosyal refah fonksiyonu oluşturmanın aslında imkansız olmasıdır. Sosyal refah fonksiyonu yaklaşımının pratik değerini ortadan kaldıran bu eleştiri, Nobel iktisat ödülü sahibi Amerikalı iktisatçı Kenneth J. Arrow tarafından ileri sürülmüştür. Arrow ‘a göre bir sosyal refah fonksiyonunun bireysel tercihleri yansıtmasının beş koşulu vardır;
- Bireysel tercihler gibi sosyal ( toplumsal ) tercihler de tamlık ve geçişlilik özelliklerine sahip olmalıdır.
- Bireysel tercihler ile sosyal refah tercihleri birbirlerinden bağımsız bir biçimde dayatılmamalıdır.
- Toplum A durumunu B durumuna sadece bir kişi istiyor diye tercih etmemelidir: Sosyal refah tercihleri bir kişinin ( diktatör ) tercihlerine dayanmamalıdır.
- Eğer bireyler farklı durumlar arasından A ve B durumlarını tercih etmişlerse ve daha sonra diğer kişilerin A tercihlerinde bir eksilme olmadan diğer kişi ya da daha fazla kişinin A tercihi değişip B durumunu tercih etmeleri şeklinde değişmişse, sosyal açıdan A tercihi B tercihine göre yine tercih edilir.
- Bir sosyal refah tercihinin diğerine göre sıralaması alternatif tercihlerden bağımsızdır: Eğer A, B, C gibi üç durum söz konusu iken A durumu B durumuna ve B durumu C durumuna tercih edilmişse, C durumu ortadan kalktığında A durumu B durumuna yine tercih edilir.
Arrow ‘a göre bu koşullardan biri ihmal edilmeden bir sosyal tercih fonksiyonu oluşturmak mümkün değildir ve bu husus Arrow imkansızlık teoremi diye nitelendirilir. Arrow imkansızlık teoreminin basit bir örneği aşağıdaki tabloda gösterilmiştir;
| Kişiler | Tercihler | ||
| A | B | C | |
| I | 1 | 2 | 3 |
| II | 2 | 3 | 1 |
| III | 3 | 1 | 2 |
Kişilerin sosyal refah tercihleri konusunda farklı tercihlere sahip oldukları tabloda, üç kişinin üç tercihe sahip oldukları varsayılmıştır. Tabloya göre birinci kişinin, birinci, ikinci, üçüncü tercihleri sırasıyla A, B, C ‘dir. Buna karşılık ikinci kişinin birinci, ikinci, üçüncü tercihleri C, A, B ‘dir. Üçüncü kişinin birinci, ikinci ve üçüncü tercihleri ise B, C ve A ‘dır. Bu durumda A ve B durumları arasındaki oylama sonucu, birinci kişi ve ikinci kişi A için üçüncü kişi ise B için oy kullanır ve dolayısıyla A durumu B durumuna tercih edilir: A B. Buna karşılık B ve C durumları arasındaki oylama sonucunda, birinci ve üçüncü kişi B için ikinci kişi ise C için oy kullanır ve dolayısıyla da B durumu C durumuna tercih edilir: B C. Son olarak A ve C durumları arasındaki oylama sonucunda, ikinci ve üçüncü kişi C için birinci kişi ise A için oy kullanır ve C durumu A duruma tercih edilir: C A. Böylece de 1 numaralı geçişlilik koşulu ihlal edilir.
Arrow’un İmkansızlık Teoremi, sosyal tercih teorisi ve kamu ekonomisi alanında temel bir dönüm noktasıdır. Bu teorem, çoğunluk oylaması veya benzeri demokratik mekanizmalarla toplumsal tercih sıralaması yapılmaya çalışıldığında, belirli makul koşullar altında tutarlı bir sonuç elde etmenin mümkün olmadığını matematiksel olarak kanıtlar. Bu, pratikte “herkesin adil ve rasyonel olarak kabul edeceği bir seçim yöntemi yoktur” anlamına gelir.
Teoremin önemi, sadece teorik bir çerçeve sunmasında değil, aynı zamanda gerçek dünyadaki karar alma süreçlerine ışık tutmasında yatar. Örneğin, seçim sistemleri, referandumlar, bütçe tahsisleri veya kamu politikası öncelikleri belirlenirken, farklı grupların farklı sıralamaları ve öncelikleri olduğunda hangi kararın “toplumsal olarak en iyi” olduğuna dair nesnel bir yöntem geliştirmek zordur. Arrow’un çalışması, seçim sistemlerinin tasarımında neden her yöntemin kendi içinde avantaj ve dezavantajlar barındırdığını gösterir.
Teoremin temel sonucu, en az üç alternatifin olduğu ve bireylerin tercihlerinin serbestçe değişebildiği durumlarda, hem diktatörlükten kaçınan hem de mantıksal tutarlılığa sahip bir sosyal tercih fonksiyonunun oluşturulamayacağını ortaya koyar. Bu nedenle, demokratik sistemler genellikle bazı koşullardan ödün verirler. Örneğin, bazı seçim sistemleri geçişlilikten taviz verirken, bazıları bireysel tercihlerden bağımsızlık ilkesini esnetebilir.
İktisat politikası açısından bu teorem, Pareto optimalite gibi refah kriterlerinin tek başına yeterli olmadığını, çünkü Pareto kriterinin hangi optimal çözümün “daha iyi” olduğunu belirlemede yetersiz kaldığını gösterir. Dolayısıyla, politika yapıcılar sadece ekonomik verimlilik değil, aynı zamanda siyasi meşruiyet, toplumsal uzlaşı ve temsil gibi faktörleri de dikkate almak zorundadır.
Arrow’un teoremi ayrıca oyun teorisi, kamu tercihi teorisi ve anayasa iktisadı alanlarında geniş yankı bulmuştur. James Buchanan ve Gordon Tullock gibi kamu tercihi teorisyenleri, bu teoremi demokratik süreçlerin sınırlarını ve siyasi pazarlıkların kaçınılmazlığını açıklamakta kullanmışlardır.
Matematiksel olarak, teoremin dayandığı ispat yöntemleri tercih sıralamalarının kombinatoryal özelliklerine dayanır. Her bireyin alternatifler üzerinde bir sıralaması vardır ve bu sıralamalar toplumsal bir sıralamaya dönüştürülmek istenir. Ancak bu dönüşüm, beş koşulun tamamını aynı anda sağlayamaz. Bu koşullar ihlal edilirse, bazı sistemler pratikte çalışabilir; ancak bu durumda da belirli adalet veya rasyonalite ilkelerinden vazgeçilmiş olur.
Teoremin uygulamada yarattığı sonuçlardan biri de, karar alma süreçlerinin şeffaflığı ve katılımcılığının tek başına “mükemmel” sonuçlar üretmeyeceğinin anlaşılmasıdır. Demokrasi, Arrow’un teoreminin işaret ettiği sınırlara rağmen, toplumsal uzlaşıyı en üst düzeye çıkaran yöntemlerden biri olarak kabul edilir. Ancak bu sınırlılıkların farkında olarak sistem tasarlamak, politika ve seçim mühendisliği açısından kritik önemdedir.
Sonuç olarak, Arrow İmkansızlık Teoremi, sosyal bilimlerde “kusursuz çözüm” arayışının neden çoğu zaman başarısızlığa mahkûm olduğunu açıkça ortaya koyar. Bu teorem, seçim sistemlerinden kamu politikalarına kadar geniş bir yelpazede, karar verme mekanizmalarının tasarımında temel bir referans noktası olmaya devam etmektedir.