Enflasyon ve hasıla düzeyi arasındaki ilişki, dinamik toplam arz – dinamik toplam talep analizi yerine Phillips eğrisi analizi yardımıyla da incelenebilir. 1926 yılında Amerikalı iktisatçı Irving Fisher ve daha sonra 1958 yılında Avusturalyalı iktisatçı A.W.Phillips tarafından enflasyon ile hasıla – istihdam düzeyi arasındaki ilişki incelenmiştir.
İngiltere’de 1861 – 1957 döneminde işsizlikle nominal ücret haddindeki değişmeler arasında nasıl bir ilişki olduğunu araştıran Phillips, söz konusu dönemde işsizlik haddi ile nominal ücret büyüme haddi arasında ters yönlü bir ilişki olduğu ( işsizlik haddi azalınca nominal ücret büyüme haddinin arttığı, işsizlik haddi artınca nominal ücret büyüme haddinin düştüğü ) ve işsizlik haddi yüzde 5.5 olunca ücret enflasyon haddinin sıfır olduğu sonucuna ulaşmıştır. İzleyen yıllarda Phillips ’in ulaştığı bu sonuç, enflasyon ücret haddindeki artışlardan etkilendiği hesaba katılarak aşağıdaki grafikte gösterilmiştir.
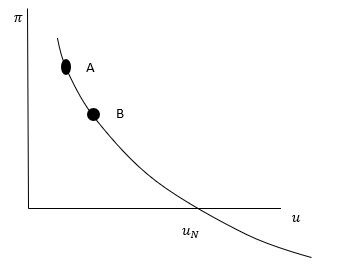
Grafikte yer alan Phillips eğrisi denilen negatif eğimli eğri, işsizlik haddi ile enflasyon haddi arasında bir değiş – tokuş olduğunu ve dolayısıyla da hükümetlerin daha yüksek bir işsizlik haddi karşılığında enflasyon haddini düşürmek ( A ==> B ) veya tam tersini yapmak ( daha yüksek bir enflasyon haddi karşılığında işsizlik haddini düşürmek ( B ==> A ), imkanına sahip olduklarını ifade eder. Phillips eğrisi denklemi aşağıdaki gibidir;
π = -y(U – Un)
Phillips eğrisi 1960’ların sonlarından itibaren başta Milton Friedman olmak üzere bazı iktisatçılar tarafından sertçe eleştirilmiştir. Bu eleştirilerin yöneldiği nokta ise, Phillips eğrisinde işsizlikle ücret – fiyat enflasyonu arasındaki ilişkinin nominal ücret üzerinden kurulmuş ve dolayısıyla da emek arzının nominal ücretin bir fonksiyonu olduğunun kabul edilmiş olmasıdır. Genel Teoride de benimsenen bu yaklaşımın yetersizliği anlaşılınca, iktisatçılar emek arzının reel ücretin bir fonksiyonu olduğunu, fakat gerçekleşen fiyat düzeyi konusunda tam bilgiye sahip olmayan işçilerin beklenen fiyat üzerinden emek arz ettiklerini kabul etmişlerdir: Ls= f(W/Pe) Bu yaklaşım altında Phillips eğrisinin matematiksel biçimi aşağıdaki gibidir;
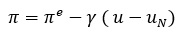
İki denklem arasındaki fark, analize fiyat bekleyişlerinin sokulmuş olmasıdır. Bu nedenle son denklemin içerdiği Phillips eğrisine ‘bekleyişlerin dahil edildiği Phillips eğrisi’ denir.
Bekleyişlerin dahil edildiği Phillips eğrisi denkleminde gerçekleşen enflasyon haddi beklenen enflasyon haddinden büyük olduğunda, işsizlik haddi doğal işsizlik haddinden küçük olur:
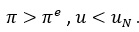
Buna karşılık gerçekleşen enflasyon haddi beklenen enflasyon haddinden küçük olduğunda, işsizlik haddi doğal işsizlik haddinden büyük olur:
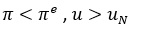
Her alternatif beklenen enflasyon haddine tekabül eden farklı bir Phillips eğrisi olduğundan, beklenen enflasyon haddini gerçekleşen enflasyon haddine eşit kılan ve dolayısıyla da işsizlik haddini doğal işsizlik haddine eşit olmasını sağlayan ;
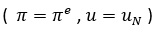
çok sayıda enflasyon haddi vardır. Her alternatif enflasyon haddinde ;
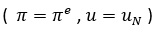
olmasını sağlayan enflasyon hadlerinin geometrik yerine, ‘uzun dönem Phillips eğrisi’ denir. Buna karşılık beklenen enflasyon haddinin gerçekleşen enflasyon haddinden farklı olduğu ve dolayısıyla da işsizlik haddinin doğal işsizlik haddine eşit olmadığı;
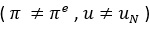
noktaların geometrik yerine ‘kısa dönem Phillips eğrisi’ denir. Kısa dönem Phillips eğrisi, kısa dönemde enflasyon haddi ile işsizlik haddi arasındaki bir değiş – tokuşun olduğunu, orijinal Phillips eğrisinin kısa dönemde geçerli olduğunu ifade eder.
